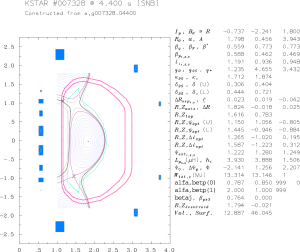
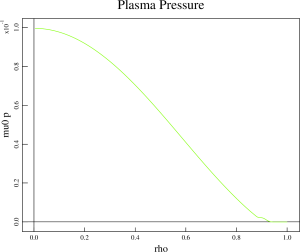
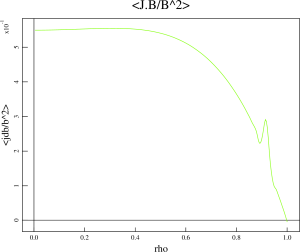
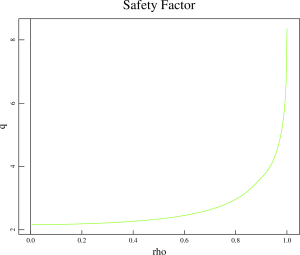
Extended MHD analysis of the pedestal region of the KSTAR discharge 7328
In order to identify minimum MHD model sufficient for nonlinear MHD analysis of KSTAR discharges, the following models in the NIMROD code were considered:
- Resistive MHD
- Lundquist number
- The Spitzer resistivity is used
- No parallel viscosity or gyro-viscosity
- No particle diffusivity, hyper-diffusivity or hyper-resistivity
- Lundquist number
- Resistive MHD with drifts
- Parallel viscosity and gyro-viscosity are enabled
- Particle diffusivity is enabled
- No hyper-diffusivity
- Two-fluid MHD
- Two-fluid two-temperature MHD
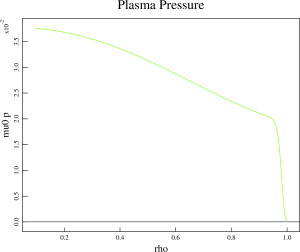
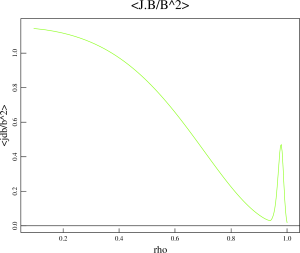
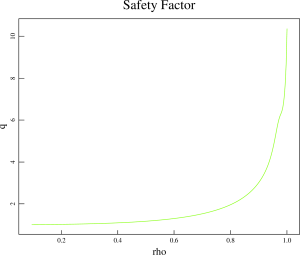
Equilibria generated for the BOUT++ stability analysis and provided by Minwoo have used in this NIMROD analysis.
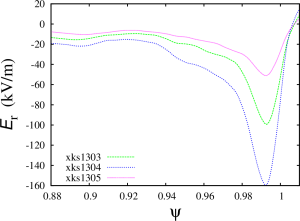
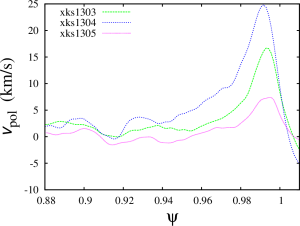
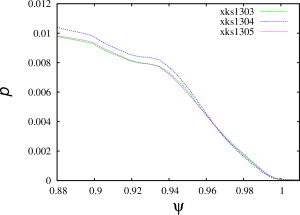
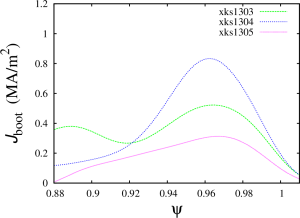
The simulation results below are given for the equilibriun number #3 from the set of equilibria obtained from Minwoo Kim on August 31. The NIMROD grid in these simulation is 72×512 with polynomial degree of 6.
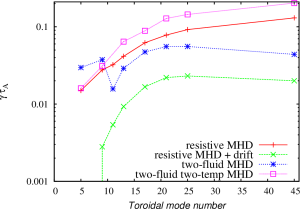
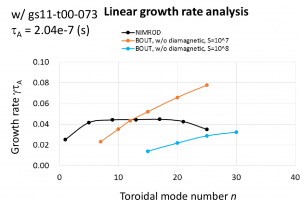
The spectrum of the most unstable toroidal modes is different comparing to the predictions produced by Minwoo using the BOUT++ code. The ELM model that Minwoo uses in his simulations is somewhat similar to the restive MHD model with drifts in the NIMROD code. The NIMROD results are very moderately peaked around n=20-30, while the BOUT++ results showed the pecking for lower toroidal mode numbers. The two fluid results in NIMROD show better peaking for n=20-25. However, the modes remain rather unstable for n=45. The nonlinear simulations that would include first 45 toroidal modes might still be underresolved. For the two-fluid nonlinear NIMROD simulations, it is better to select equilibrium with the pressure profiles somewhat more relaxed in the H-mode pedestal region and with the larger bootstrap fraction so that lower n modes are more unstable.
The eigenmode structure for low- and high- toroidal mode numbers are found different in the two fluid simulations. The unstable lower toroidal mode numbers are found to be localized in the high filed side region, while the higher toroidal mode numbers are found to have more ballooning like nature. The transition between these two distinguishably different regions is found around n=9.
The inclusion of two-temperature effects is found to affect the mode sprectrum and mode structure. The toroidal mode number of the most unstable modes is larger than the maximum toroidal mode number investigated in this study.
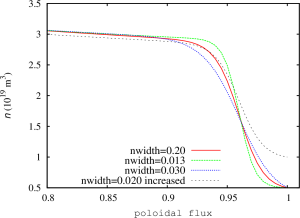
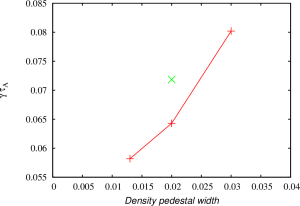
The modes found in the two-temperature NIMROD simulations are sight more shifted towards the pedestal top comparing to the modes found in the two-fluid simulations. It looks like that the inclusion of two-temperature effects destabilizes a different types of modes comparing to the modes found in the two-fluid simulations. In order to investigate the properties of these modes, the density profiles in the original equilibrium has been altered so that the density gradient in the pedestal region has been changed. The pressure profile is not affected by this change. The density width has been changed from 0.013 to 0.03 in this scan. In addition, the density at the separatrix has been increased to investigate how this change will effect the growth rates in two-temperature two-fluid simulations. Note that the resistivity in the density width scan remains modestly affected. However, the resistivity in the simulation with the increased separatrix density is strongly effected because the separatrix temperature has been reduced to keep the pressure profiles unchanged.
The growth rates for the first three cases are found comparable to each other in the resistive MHD and two-fluid simulations. The growth rates for the fourth case are found significantly larger than the growth rates in three other cases in the resistive MHD NIMROD simulations. It is also found that the the increased density gradient result in lower growth rates in the two-temperature NIMROD simulations. Such behavior is typical for ITG modes that are destabilized when the ratio of temperature gradient to the density gradient is increased.